Planispirální ulity a počítačové modely ulit (diskoidálních – scheibenförmig – discoidal)
Vedle nádhery spirály, kterou vytváří ulita, jsou plži fascinující i prostorovým růstem savých ulit – růstem, který je možné matematicky modelovat.
- Shell Space – The Snugness Condition (yellow model)
David Raup model (adopted by Richard Dawkins)
W (the rate of growth of the spiral), the verm
T (the rate of creep parallel to the spiral axis)
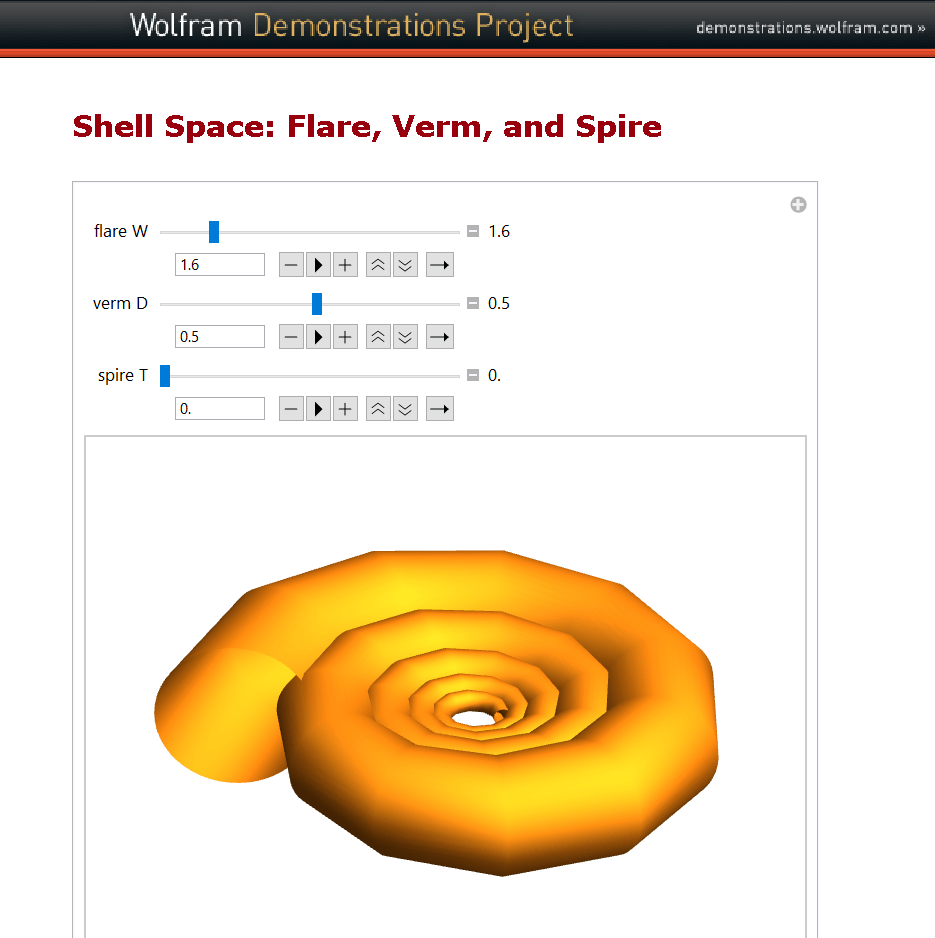
- Shell Space: Flare, Verm, and Spire (yellow model)
W (the rate of growth of the spiral)
D (the „tightness“ of the shell cavity)
T (the rate of creep parallel to the spiral axis)
- Shell Parameter Space (green model)
Jayna Resman, Michelle Winerip, Elizabeth Cowdery, and Allison Reed-Harris
Raup a další
Raup v roce 1962 vyvinul čtyřparametrový počítačový model, který na osciloskopu generoval „digitální plášť“. Parametry jsou poměr velikostí (W) po sobě jdoucích generujících křivek, vzdálenost (D) generující křivky od osy a podíl (T) výšky jedné generující křivky, kterou pokrývá každá následující otočka. Nastavením W a T vzniknou tvary připomínající mlže ústřice , zahradní šneky a piskoře. Většina teoretických forem ulit se v přírodě nevyskytuje. (Raup v roce 1962). Přesto byly matematické modely růstu ulit v 90. letech 20. století zpochybněny. (Hutchinson v roce 1989).
Další faktory
Škálovací exponent tloušťky skořápky jako morfologický parametr. Škálovací exponent má drastický vliv na optimální návrh tvaru skořápky. Jednotný způsob je výsledkem optimálního využití zdrojů materiálu skořápky, zatímco izometrický růst tloušťky vede k nemožně těsnému svinování (Okabe, Yoshimura, 2017). Savazzi v roce 1985 vyvinul simulátor SHELLGEN, který k modelování ontogeneze schránek měkkýšů využívá přibližné diferenční rovnice. (Savazzi, 1985).
Obvyklé tvary
Variabilita tvaru schránek suchozemských měkkýšů má velkou genetickou složku. Větší plži jsou často spojeni s vlhčími podmínkami. Relativní plocha apertury bývá v sušších podmínkách menší. Větší plži mají tendenci mít vyšší rychlost rozšiřování závitů. Relativní výška ulity u jednotlivých druhů plžů souvisí s úhlem substrátu, na kterém probíhá činnost. (Goodfriend, 1986)
Raup and others
Raup in 1962 developed a four-parameter computer model that generated „digital shell“ on an oscilloscope. Parameters are the size ratio (W) of successive generating curves, the distance (D) of the generating curve from the axis, and the proportion (T) of the height of one generating curve that is covered by each subsequent turn. Adjustment of W and T produces forms reminiscent (prom the right) bivalve oysters , garden snails and whelks. The majority of theoretical shell forms do not occur in nature. (Raup in 1962). Still, mathematical models of shell growth were questioned in the 1990s. (Hutchinson, 1989).
Other factors
Other factors also play a role: The scaling exponent of shell thickness as a morphological parameter. The scaling exponent has a drastic effect on the optimal design of shell shapes. Unified manner are a result of optimal utilization of shell material resources, while isometric growth in thickness leads to impossibly tight coiling (Okabe, Yoshimura, 2017). Savazzi in 1985 developed simulator SHELLGEN that uses approximate difference equations to model the ontogeny of molluscan shells. (Savazzi, 1985).
Variation in land-snail shell form has a large genetic component. Larger snails are often associated with moister conditions. Relative aperture area tends to be smaller under drier conditions. Larger snails tend to have higher whorl expansion rates. Relative shell height of snail species relates to the angle of the substrate on which activity occurs. (Goodfriend, 1986)
References:
Goodfriend, Glenn A. (1986). Variation in Land-snail Shell form and Size and its Causes: a Review. Systematic Biology. Vol. 35. Iss. 2, pp. 204–223, doi.org/10.1093/sysbio/35.2.204
Hutchinson, J. M. C. (1989). Control of Gastropod Shell Shape; The Role of the Preceding Whorl. J. theor. Biol. Vol. 140, pp. 431-444.
Liew T-S, Schilthuizen M (2016) A Method for Quantifying, Visualising, and Analysing Gastropod Shell Form. PLoS ONE 11(6): e0157069. https://doi.org/10.1371/journal.pone.0157069
Okabe, Takuya & Yoshimura, Jin. (2017). Optimal designs of mollusk shells from bivalves to snails. Scientific Reports. 7. 42445. 10.1038/srep42445.
Ramsden, Phil (2009). „Shell Space: Flare, Verm, and Spire“ from the Wolfram Demonstrations Project. http://demonstrations.wolfram.com/ShellSpaceFlareVermAndSpire/
Raup, David M. (1962). Computer as Aid in Describing Form in Gastropod Shells. Science (New York, N.Y.). 138. 150-2. 10.1126/science.138.3537.150.
Resman, Jayna, Winerip, Michelle, Cowdery, Elizabeth and Reed-Harris, Allison (2011). „Shell Parameter Space“. http://demonstrations.wolfram.com/ShellParameterSpace/ . Wolfram